SÍGUENOS EN YOUTUBE

ÚNETE A NOSOTROS. ¡SOMOS EL CLUB MATEMÁTICO!



Activar correo Institucional: I.E. 20 DE JULIO

   15:28        
Procuraduría confirmó destitución e inhabilidad de docente Henry ...
La institución Educativa 20 de Julio ha creado los correos Institucionales de cada estudiante, esto con el fin de poder acceder de una manera mas agil a las herramientas de Google como lo es ClassRoom.

¿Como la activas?
Abres Gmail
para iniciar sesión debes colocar el correo, el correo esta compuesto por tu primer nombre, tu primer apellido y luego @ie20dejulio.edu.co

Por ejemplo. oscarpineda@ie20dejulio.edu.co

¿Cual es la contraseña?

La contraseña es tu documento de identidad, tarjeta de identidad o Registro civil.

IMPORTANTE: Las personas con nombres y apellidos que incluyan la letra ñ la deben reemplazar por N, por ejemplo: nuñez --> nunez 

Monomios: Partes de un monomio, monomios semejantes y Operaciones

   6:10        
☑EJERCICIOS DE ALGEBRA x² ONLINE ツ | Matemáticas en un Clic
Temas:
1. Partes de un Monomio
2. Monomios semejantes
3. Operaciones con monomios
Objetivo: Identificará  y clasificará expresiones algebraicas

 Un monomio es una expresión algebraica en la que las únicas operaciones que aparecen entre las variables son el producto y la potencia de exponente natural

 {2x^{2}y^{3}z}

Partes de un monomio

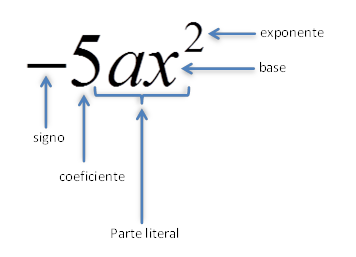
ÁLGEBRA - Monomios, polinomios y sus operaciones - academia JAF ...
Ejemplos:
1El coeficiente del monomio {3x^{3}y^{2}z} es {3}
 2El coeficiente del monomio {\displaystyle\frac{3}{4}xy^{2}z} es {\displaystyle\frac{3}{4}}
 3El coeficiente del monomio {{x^{2}z} es {1}

Parte literal

 La parte literal está constituida por las letras y sus exponentes.
Ejemplos:
1La parte literal del monomio {3x^{3}y^{2}z} es {x^{3}y^{2}z}
2La parte literal del monomio {y^{2}z} es {y^{2}z}
 3La parte literal del monomio {2abc} es {abc}
 4El monomio {5} no tiene parte literal
 5La parte literal del monomio {x} es {x}

Grado

 El grado de un monomio es la suma de todos los exponentes de las letras o variables.
Ejemplos:
1El grado del monomio {2x^{2}y^{3}z} es: {2+3+1=6}
 2El grado del monomio {{x^{2}z} es: {2+1=3}
 3El grado del monomio {2abc} es: {1+1+1=3}
 4El grado del monomio {5} es: {0} (se podría escribir como {5x^{0}})
Monomios semejantes: Dos monomios son semejantes cuando tienen la misma parte literal.
Ejemplos:
1{2x^{2}y^{3}z} es semejante a {5x^{2}y^{3}z}

2{5xz} es semejante a {xz}

3{4a^{3}z^{2}} es semejante a {a^{3}z^{2}}

Suma y resta de monomios
Para poder sumar dos o más monomios estos han de ser monomios semejantes, es decir, monomios que tienen la misma parte literal.
La suma de monomios es otro monomio que tiene la misma parte literal y cuyo coeficiente es la suma de los coeficientes.

{ax^{n}+bx^{n}=(a+b)x^{n}}
Ejemplos:
1{2x^{2}y^{3}z+3x^{2}y^{3}z=(2+3)x^{2}y^{3}z=5x^{2}y^{3}z}

2{4xy + 3xy - 5xy = 2xy}

3{4x - 5x - 3x + 2x = -2x}
Si los monomios no son semejantes, al sumarlos, se obtiene un polinomio.

Ejemplo:
1{2x^{2}y^{3}}+3x^{2}y^{3}z}

Producto de un número por un monomio


El producto de un número por un monomio es otro monomio semejante cuyo coeficiente es el producto del coeficiente del monomio por el número.

Ejemplos:
1{5\cdot (2x^{2}y^{3}z)=10x^{2}y^{3}z}

Es común que para indicar la multiplicación no pongamos el signo por entre el número y el paréntesis

2{4(2x^{2}y^{3}z)=8x^{2}y^{3}z}

Multiplicación de monomios


La multiplicación de monomios es otro monomio que tiene por coeficiente el producto de los coeficientes y cuya parte literal se obtiene multiplicando las potencias que tengan la misma base, es decir, sumando los exponentes.

{\left(ax^{n}\right)\left(bx^{m}\right)=(ab)x^{n+m}}

Ejemplos:
1{\left(5x^{2}y^{3}z\right)\left(2y^{2}z^{2}\right)=(2\cdot 5)x^{2}y^{3+2}z^{1+2}=10x^{2}y^{5}z^{3}}

2{\left(4x\right)\left(3x^{2}y\right)=(4\cdot 3)x^{1+2}y^{1}=12x^{3}y}

División de monomios


Sólo se pueden dividir monomios cuando el grado del dividendo es mayor o igual que el del divisor.

La división de monomios es otro monomio que tiene por coeficiente el cociente de los coeficientes y cuya parte literal se obtiene dividiendo las potencias que tengan la misma base, es decir, restando los exponentes

{\left(ax^{n}\right)\left(bx^{m}\right)=(a:b)x^{n-m}}

Ejemplo:
1{\left(6x^{3}y^{4}z^{2}\right) : \left(3x^{2}y^{2}z^{2}\right)=(6: 3)x^{3-2}y^{4-2}z^{2-2}=2x^{1}y^{2}z^{0}=2xy^{2}}

Si el grado del divisor es mayor, obtenemos una fracción algebraica

Ejemplo:
1{\left(6x^{3}y^{4}z^{2}\right) : \left(3x^{5}y^{2}z^{4}\right)=(6: 3)x^{3-5}y^{4-2}z^{2-4}=2x^{-2}y^{2}z^{-2}=\displaystyle\frac{2y^{2}}{x^{2}z^{2}}}

ECUACIONES - LENGUAJE ALGEBRAICO

   6:24        
Ecuaciones lineales.


Una ecuación es una igualdad matemática entre dos expresiones, denominadas miembros y separadas por el signo igual, en las que aparecen elementos conocidos y datos desconocidos o incógnitas, relacionados mediante operaciones matemáticas.

¿Como se resuelve una ecuación?
Observa el video y luego regresa a la pagina


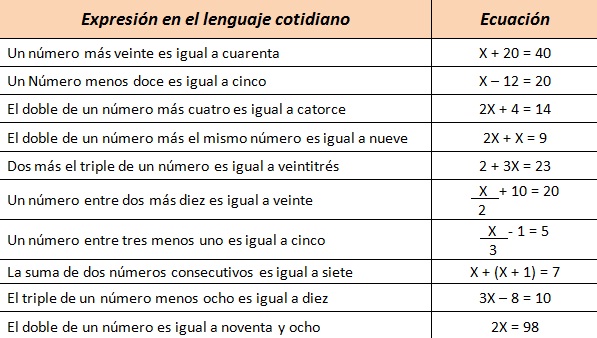
Lenguaje Algebraico 
El lenguaje algebraico es una forma de traducir a símbolos y números lo que normalmente tomamos como expresiones particulares. De esta forma se pueden manipular cantidades desconocidas con símbolos fáciles de escribir lo que permite simplificar teoremas, formular ecuaciones e inecuaciones y el estudio de cómo resolverlas. Este lenguaje nos ayuda a resolver problemas matemáticos mostrando generalidades. 

EL lenguaje algebraico nace en la civilización musulmana en el periodo de AL-Khwarizimi durante la edad media. Su función principal es establecer y estructurar un idioma que ayuda a generalizar las distintas operaciones que se desarrollen dentro de la aritmética donde solo ocurren los números y sus operaciones aritméticas elementales (+ -x %). Una expresión algebraica es una cadena de representaciones perteneciente al lenguaje algebraico, el cual puede contener variables, números, así como también operaciones aritméticas. El Término, es una expresión algebraica donde hay solo operaciones de multiplicación y división de letras y números, tanto el numero como la letra puede estar elevado a una potencia.

El termino independiente solo consta de un valor numérico, en tanto los términos semejantes son los que tienen debidamente la misma parte de letras (parte literal) y varían solo su coeficiente. Estos solo se pueden sumar y restar, si los términos no son semejantes ya no es posible, lo que si es posible es dividir o multiplicar todo tipo de termino. El grado de un término puede ser de grado absoluto, lo cual es la suma de los exponentes de cada letra, o puede ser un término de grado relativo en lo cual se toma en cuenta la letra y su exponente.

Expresión en el lenguaje cotidiano





UTILIDAD DE LOS NÚMEROS ROMANOS

   17:00        
Hoy en día se usan los números romanos en muchas ocasiones, como para nombrar a los siglos (siglo XXI) , a los reyes (Felipe VI), a los papas (Francisco I), los aniversarios, las olimpiadas, los congresos, los capítulos, en los relojes, las materias (Matemáticas I), los actos de las obras de teatro,...
HISTORIA DE LOS NÚMEROS ROMANOS

Los números romanos eran utilizados en el Imperio Romano. Era un sistema que empleaba siete letras mayúsculas (I, V, X, L, C, D y M), y cada una representaba un valor numérico. Según se combinaban representaban un número diferente. Este sistema de numeración se sustituyó por la numeración actual que es arábiga, proviene de la India y fue traída por los árabes.

NUMERACIÓN ROMANA

El valor de los símbolos es:

I.......1
V.......5
X.......10
L....... 50
C.......100
D....... 500
M..... 1000



Hay diferentes reglas para escribir estos números.
REGLA DE LA SUMA
Cuando se coloca una letra a la derecha que tenga igual o menor valor que la anterior y se le suma a ésta su valor.
VI....5+1=6
XII....10+2=12

REGLA DE LA RESTA
Las letras I, X y C se colocan a la izquierda de otra que tenga mayor valor y se restan.
Pero..... hay una serie de condiciones:
La letra I sólo puede restar a V y a X. (Resta 1) Ej: IV= 5-1=4
La letra X sólo puede restar a L y a C. (Resta 10) Ej: XL= 50-10=40
La letra C sólo puede restar a D y a M. (Resta 100) Ej: CM=1000-100=900
Las letras D, L y V no se pueden colocar a la izquierda para restar.

REGLA DE REPETICIÓN
Las letras M, C, X, I se pueden repetir y colocar hasta tres veces seguidas.
Ej: CCCLIII= 353

REGLA DE LA MULTIPLICACIÓN
Esta regla se usa para escribir números mayores de 3999.
Si ponemos una raya horizontal encima del valor, este queda multiplicado por mil.
Si ponemos dos rayas horizontales encima del valor, este queda multiplicado por un millón.
Suscribirse a: Comentarios ( Atom )