En la película Una mente maravillosa, el brillante matemático estadounidense John Nash (interpretado por Russell Crowe) está en un bar con sus compañeros de la Universidad de Princeton cuando se le ocurre un plan para intentar ligar con un grupo de chicas entre las que destaca una rubia que llama la atención de todos ellos. La estrategia que traza es matemática aplicada pura. Está basada en la denominada teoría de juegos, un área que permite estudiar y predecir el comportamiento de los individuos involucrados en una situación a partir de las interacciones entre ellos, sus estrategias y los conflictos de intereses. El propio Nash, galardonado con el Premio Nobel de Economía en 1994, contribuyó decisivamente a esta rama de las matemáticas con sus investigaciones.
La teoría de los juegos fue desarrollada inicialmente como una herramienta para ayudar a comprender aspectos relacionados con la economía, pero sus usos se han ido extendiendo a otros campos, como la psicología, la biología o la sociología. Es por ello un ejemplo de cómo las matemáticas, que siempre han servido para explicar y comprender el mundo, están siendo aplicadas a infinidad de áreas y cada vez tienen un mayor peso en la economía. Los matemáticos, que tradicionalmente no solían tener mucho contacto con la realidad, forman parte de plantillas de empresas muy diversas.
«Las matemáticas tienen muchísimas aplicaciones en la vida diaria», afirma Manuel de León, director del ICMAT y presidente de este congreso en el que se ha propiciado el acercamiento entre los investigadores y la industria: «Muchos son reacios a hacer transferencia de conocimiento. Por supuesto, hay matemáticos que están haciendo investigación básica muy importante y no tienen por qué hacer transferencia. Pero el objetivo es ampliar el abanico de empleos y que los matemáticos no sólo se dediquen a la investigación económica, a la docencia o a la banca», señala De León.
Las mates te rodean desde el momento en que cruzas las puertas automáticas de tu supermercado favorito.
Efectivamente, las puertas y el detector de metales que cruzas a la entrada de la tienda están compuestos por sistemas electrónicos que no podrían haber sido diseñados sin las matemáticas.
Después, empiezas a hacer la compra y tu carrito se llena de productos que tienen etiquetas (con el famoso código de barras que indica, gracias a sus cifras, el fabricante del producto y su código específico); a continuación te diriges a la caja, en donde cada etiqueta se escanea con láser para que el precio final aparezca en la pantalla.
Por último, realizas el pago con tarjeta de crédito o en efectivo.
Todas estas etapas, todas estas operaciones, han utilizado numerosas nociones de matemáticas.
Durante tu compra podrás observar que tu supermercado te propone ofertas o promociones con un 30% de descuento o con descuentos mayores por la compra de dos artículos.
Gracias a las matemáticas entiendes que el 10% de descuento sobre un producto y después un 20% sobre el mismo producto no genera una reducción total del 30%.
El interés de conocer algunas técnicas para calcular mentalmente y el haber estudiado los porcentajes en mates encuentran aquí toda su utilidad.
¡También necesitas las matemáticas en tu vida profesional! Incluso si se trata de un trabajo que no está relacionado con la ciencia. Una secretaria tendrá que utilizar Excel, un vendedor deberá ser capaz de calcular mentalmente y un arquitecto necesitará calcular ángulos.
Te invito a que te preguntes, ¿En que momento utilizo las matemáticas en mi vida personal?
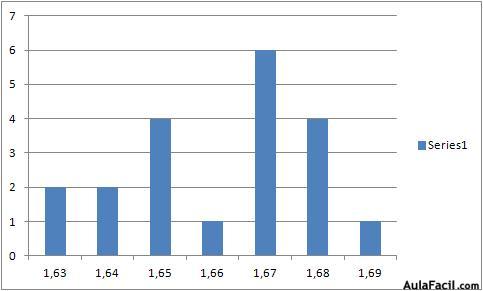
, es decir, cambiamos el numerador de signo
es 
es 
es 
es semejante a 
es semejante a 
